这篇文章是介绍神经网络中的训练方法-BP算法,算是一篇比较经典的文章,最近又自己用SIMD指令集重写一个小型的神经网络,借此机会再好好巩固一下BP算法。
使用反向传播算法训练多层神经网络的原理
本项目使用BP算法来介绍多层神经网络的训练过程,下图展示了一个包含三层神经元的网络,具有两个输入,一个输出。
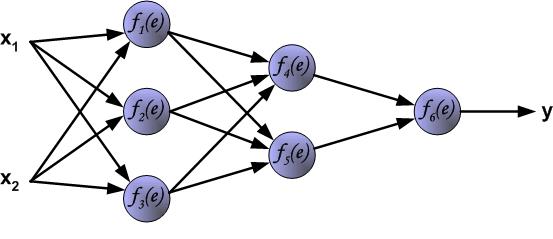
每个神经元有两个操作组成,一个是将系数(包括权重和偏置)和输入信号进行叠加,第二个是引入非线性,我们一般称之为神经元激活函数,其中 $e$ 就是叠加信号,$y=f(e)$ 为非线性部分的输出,$y$也被称为神经元的输出。
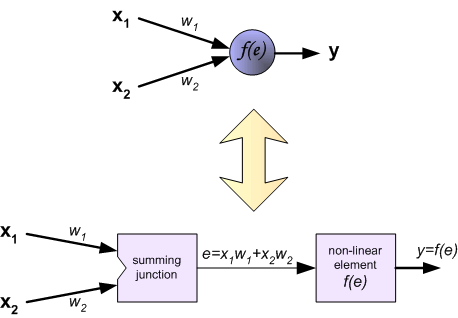
为了训练神经网络,我们需要训练集。训练集包含输入信号 $x_1$ 和 $x_2$ 以及它们对应的期望输出 $z$,网络的训练是一个迭代的过程。在每个迭代过程,都会根据当前的训练数据对神经元的系数进行调整,调整的规则如下:每一轮的训练都是从训练集的两个输入开始,经过一系列计算,我们可以得到每个神经元的输出。下图说明了信号是如何在网络中传播的,符号 $W_{(xm)n}$ 表示网络的输入 $x_m$ 和输入层的神经元 $n$ 之间的权重,符号 $y_n$ 表示神经元 $n$ 的输出。
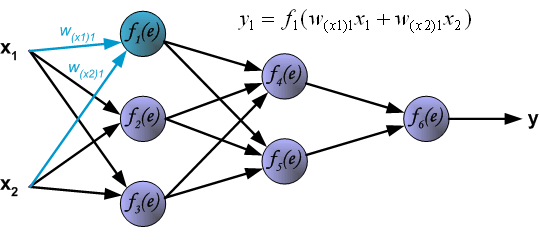
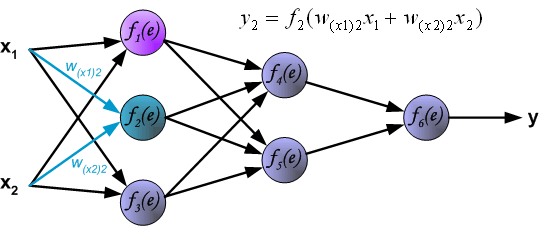
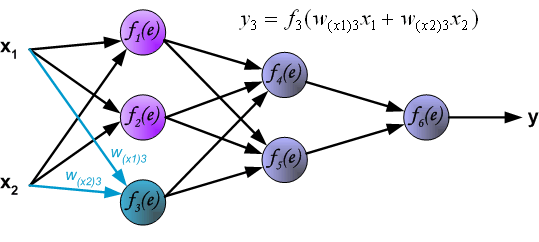
紧接着,信号传递到隐藏层,符号 $W_{mn}$ 表示神经元 $m$ 的输出和下一层的额神经元 $n$ 之间的权重。
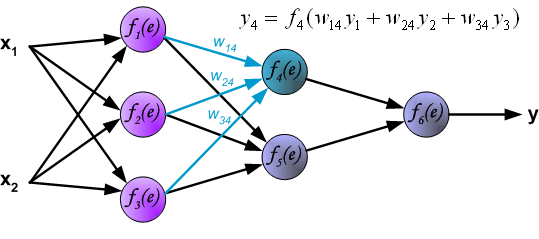
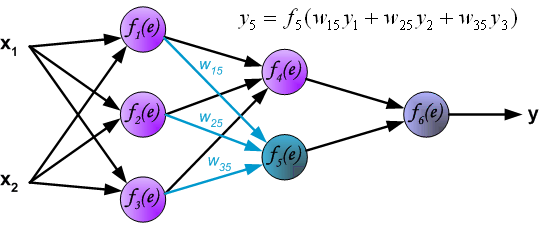
信号到达了输出层。
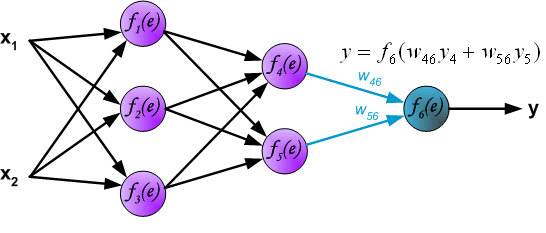
接下来,网络的输出信号 $y$ 会和训练集给出的期望输出进行对比,它们之间的差异被称为输出层的误差 $\delta$。
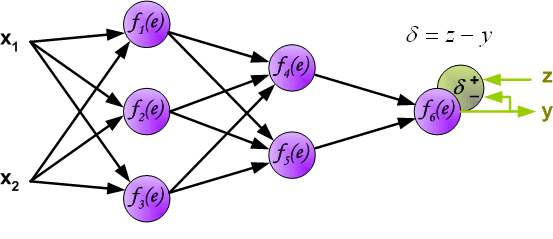
直接计算中间层的神经元的误差是不现实的,因为它们的输出值我们目前还不知道。很久以来都没有有效的方法去训练多层神经网络,直到80年代中期,反向传播算法才被提出。它的思路是将误差信号 $\delta$ (同一次迭代中)反向传播回所有神经元。
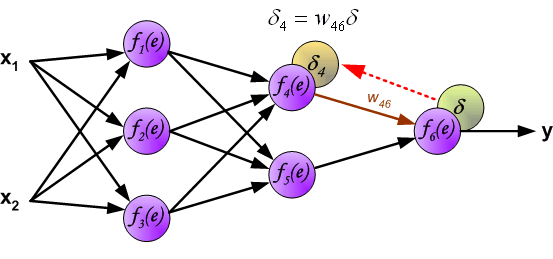
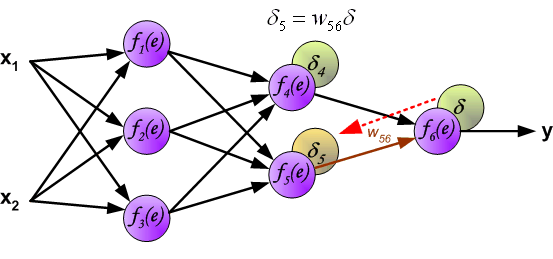
用于反向传播的系数 $W_{mn}$ 和正向计算时候的值一样(它们是共用的),只是信号的方向变了(之前是信号是从前一个神经元到下一个神经元,现在的误差信号是从下一个神经元到前一个神经元,所以才称为“反向传播”),这种操作应用与全部的神经网络层。
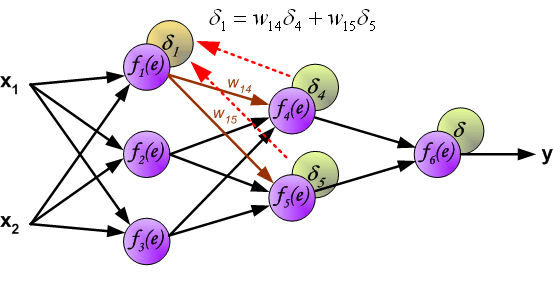
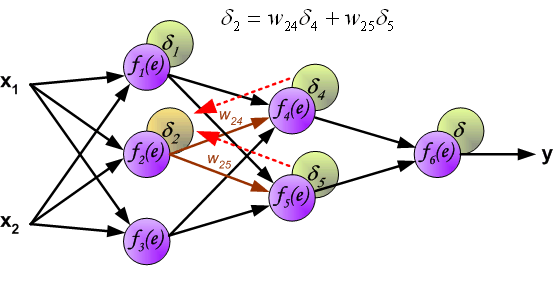
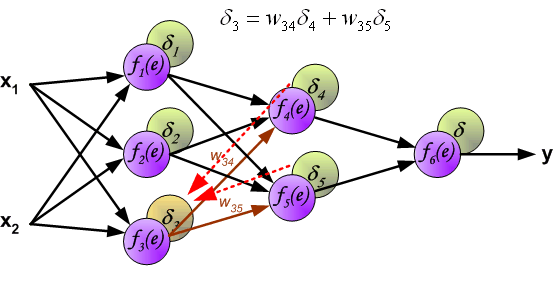
当所有神经元的误差都被计算后,它们之间的权重系数就会被更新。公式中的 $df(e)/de$ 表示激活函数的导数。
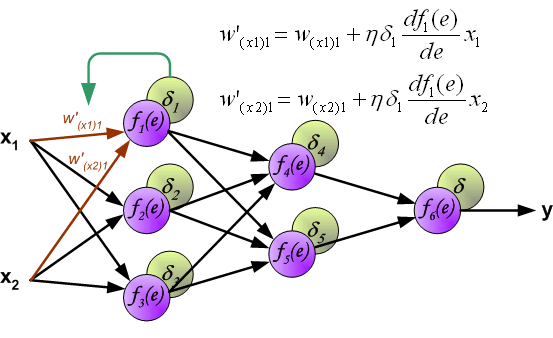
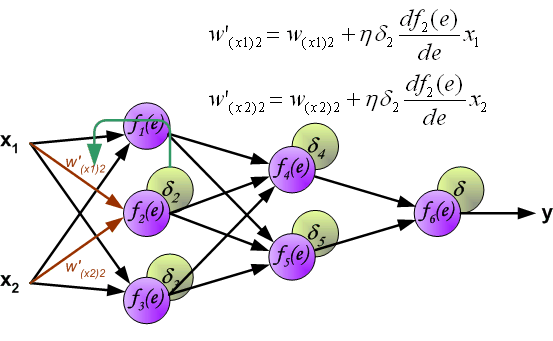
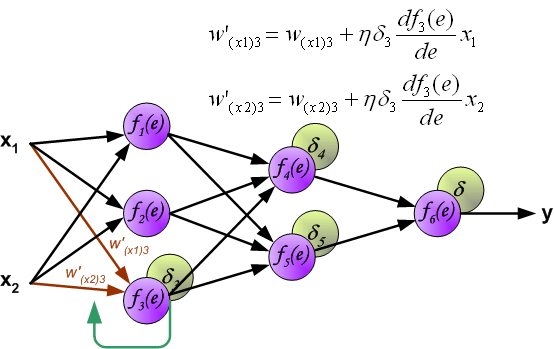
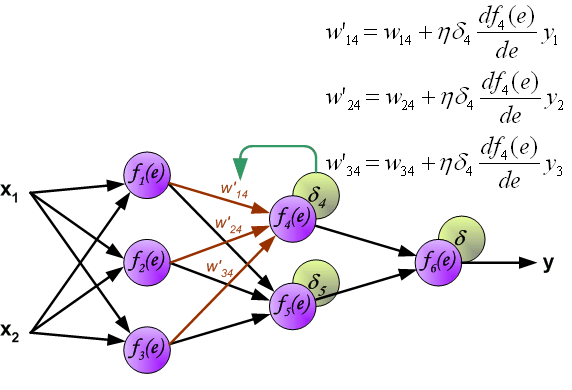
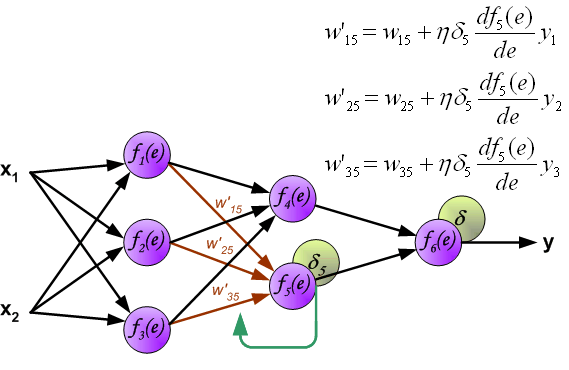
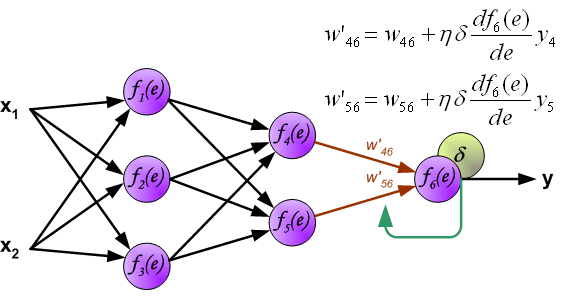
系数 $\eta$ 用来调节网络训练的速度,目前有很多方法去调节这个参数,第一种方法是在网络训练刚开始时,使用较大的 $\eta$,随着训练的进行,再逐渐减小。第二种相对复杂一点,刚开始训练时,使用较小的 $\eta$,随着训练进行,逐渐增大 $\eta$,然后再逐渐减小 $\eta$ 直到训练结束。